ВВЕДЕНИЕ В ТОЧНОСТНУЮ ТЕОРИЮ НАДЕЖНОСТИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
Смагин В.А.
Заслуженный деятель науки России,
доктор технических наук, профессор
Потенциальным источником опасности и риска в сложных системах являются их информационные ошибки. В данной статье наряду с классическим подходом построения теории надежности программного обеспечения предложен подход,
основанный на исследовании точности его операторов.
Ключевые слова:
программное обеспечение, надежность,сложность программ, ошибка, эффект накопления, точность
вычисления, распределение вероятностей, моделирование,
прогноз.
_______________________________________________________________________________
1.
ВВЕДЕНИЕ"Вычислительные машины служат, в общем, для записи чисел, для действий над ними и выдачи результата в числовой форме" [1]. Они были созданы на основе успехов математики и в интересах решения задач математики. Их преимущества - быстродействие и высокая точность вычислений - сыграли огромную роль в решении ряда важных практических задач самого различного характера.
В настоящее время практически нет такой области науки и техники, где бы не использовались эти совершеннейшие технические средства. Бурное развитие техники связи и теории информации во многом обусловлено прогрессом в области вычислительной техники. В настоящее время средства вычислительной техники служат не только для производства сложнейших и точнейших расчетов и управления различными объектами, но и для представления информации в нечисловом количественном, смысловом, виде. Однако, в каком бы виде информация ни была представлена вычислительными средствами, она всегда в своей основе является числовой, цифровой.
Дальнейшая цивилизация общества требует решения все более сложных задач. Это неизбежно приводит к лавинообразному росту сложности алгоритмов решения этих задач, программного обеспечения и самих вычислительных средств. Сложность алгоритмов и программ решения задач - неизбежный источник ошибок вычислений.
Кроме того, наши первичные измерения любых величин, данных, которые вводятся в вычислительные средства, содержат погрешности. Например, константы ? и e в компьютере, на котором набран данный текст, представлены после запятой всего лишь 14 цифровыми знаками. В результате этого, мы вынуждены обращать внимание на точность вычислений и наряду с надежностью техники заниматься надежностью вычислений.Современная теория и практика надежности программного обеспечения (точнее, надежности функционирования программно-управляемых вычислительных средств или просто вычислительных средств, действие которых не мыслимо без программ) основана на вероятностном подходе, использующем статистические данные об ошибках (исходных данных, самих программ, техники, человека-оператора)
. Она использует обширный ряд моделей и методов исследования надежности программного обеспечения (программ) [2,3]. Однако возможности такого подхода весьма ограничены из-за скудности статистических данных об ошибках программ. И, следует отметить, что этот статистический дефицит ошибок по мере усовершенствования элементной базы, техники и качества программ, ростом автоматизации, будет все более сказываться. Но это не означает, что с ошибками программ будет покончено.Любое вычисление связано с определенной точностью. Чем сложнее вычисление, тем меньше его точность. Сложное вычисление складывается из простых, малых вычислений. Сложная программа состоит из большого количества элементарных операторов. Конкретная реализация траектории вычислений обладает определенной точностью, обусловленной составом, точностью операторов и точностью округления результата вычисления каждого оператора.
Цель данной статьи обратить внимание исследователей на точностной аспект сложных вычислений, показать элементарным анализом как изменяется точность вычислений в зависимости от сложности программы, определив вероятность возникновения ошибки в простейшей, гипотетической программе, и поставить задачу исследования на точность всех операторов, из которых составляются сложные программы.
2.
ПРОСТЕЙШИЙ ЛИНЕЙНЫЙ ОПЕРАТОРРассмотрим свойства оператора
![]() . (1)
. (1)
Для простоты исследования положим, что
величины ![]() детерминированные
и произвольные, а константа
детерминированные
и произвольные, а константа ![]() - случайная величина с плотностью
распределения
- случайная величина с плотностью
распределения
![]()
![]() (2) Найдем плотность
распределения теперь уже случайной величины
(2) Найдем плотность
распределения теперь уже случайной величины ![]() она равна:
она равна:
![]() (3)
(3)
Предположим, что точность величины ![]() определена или задана как
определена или задана как
![]() или
или ![]() (4)
(4)
Тогда в вычисления вносится ошибка
из-за случайности величины ![]() Вероятность возникновения такой ошибки
равна:
Вероятность возникновения такой ошибки
равна:
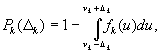 (5)
(5)
где ![]() -математическое
ожидание величины
-математическое
ожидание величины ![]() Пусть,
например,
Пусть,
например,
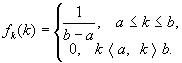 (6)
(6)
Из (1) найдем
![]() (6)
(6)
При ![]() вероятность
ошибки равна 1, а при
вероятность
ошибки равна 1, а при ![]() что
и следовало ожидать.
что
и следовало ожидать.
Поступая подобным образом, найдем вероятность
появления ошибки в выходной величине ![]() если пределы точности ее
заданы величиной
если пределы точности ее
заданы величиной ![]()
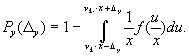 (7)
(7)
В частности, при равномерном распределении
величины ![]() (5) найдем:
(5) найдем:
![]() (8)
(8)
В дальнейшем предполагаем, что ![]() то есть точность выходной величины
равна точности представления величины
то есть точность выходной величины
равна точности представления величины ![]() Сравним (4) и (8), вводя их
отношение, при равномерной плотности:
Сравним (4) и (8), вводя их
отношение, при равномерной плотности:
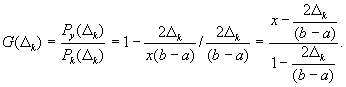 (9)
(9)
Из (9) следует, что только при ![]() вероятности обеих ошибок
одинаковы. Если
вероятности обеих ошибок
одинаковы. Если ![]() , то
вероятность ошибки на выходе оператора больше,
чем вероятность ошибки константы
, то
вероятность ошибки на выходе оператора больше,
чем вероятность ошибки константы ![]() и это преобладание будет
увеличиваться тем больше, чем будет больше
диапазон предела точности
и это преобладание будет
увеличиваться тем больше, чем будет больше
диапазон предела точности ![]() С увеличением
С увеличением ![]() степень
этого возрастания будет больше. Отсюда следует
вывод: при оговоренных условиях простейший
линейный оператор со случайным передаточным
коэффициентом увеличивает вероятность ошибки в
выходной величине. Это справедливо и в отношении
влияния на
степень
этого возрастания будет больше. Отсюда следует
вывод: при оговоренных условиях простейший
линейный оператор со случайным передаточным
коэффициентом увеличивает вероятность ошибки в
выходной величине. Это справедливо и в отношении
влияния на ![]() величины
величины ![]() когда она становится
случайной. Однако, совместное влияние
погрешностей
когда она становится
случайной. Однако, совместное влияние
погрешностей ![]() на
на ![]() здесь рассматривать не
будем.
здесь рассматривать не
будем.
Если ![]() отношение
отношение
![]() с увеличением
с увеличением ![]() уменьшается, беря свое
начало по прежнему с
уменьшается, беря свое
начало по прежнему с ![]() при
при
![]()
Рассмотрим информационное свойство
данного оператора. Энтропия случайной величины ![]()
![]() будет
равна
будет
равна ![]() а энтропия
случайной величины
а энтропия
случайной величины ![]()
![]() (10)
(10)
Из формулы (10) следует, что
неопределенность значений выходной переменной ![]() по отношению к
неопределенности
по отношению к
неопределенности ![]() возрастает
при
возрастает
при ![]() и убывает при
и убывает при ![]() Если определить
приращение количества информации на выходе
оператора по отношению ко входу, то будем иметь
[4]:
Если определить
приращение количества информации на выходе
оператора по отношению ко входу, то будем иметь
[4]:
![]() (11)
(11)
где ![]() якобиан
преобразования. Из формулы (11) следует: при
якобиан
преобразования. Из формулы (11) следует: при ![]() приращение количества
информации отрицательно, а при
приращение количества
информации отрицательно, а при ![]() положительно, что согласуется с (10).
положительно, что согласуется с (10).
В большинстве литературных источников утверждается, что количество информации не может быть отрицательным. Однако, это не согласуется с рядом источников, например [5], в котором под количеством информации понимается
![]() (12)
(12)
где ![]() вероятности
наступления события после опыта и до опыта
(апостериорная и априорная вероятности). И если
апостериорная вероятность меньше априорной, то
количество информации отрицательно. Следует
заметить, что в [6] выражение (12) понимается как не
количество информации, а ее ценность.
вероятности
наступления события после опыта и до опыта
(апостериорная и априорная вероятности). И если
апостериорная вероятность меньше априорной, то
количество информации отрицательно. Следует
заметить, что в [6] выражение (12) понимается как не
количество информации, а ее ценность.
Мы будем придерживаться определения
(12) и в качестве оправдания этого факта
рассмотрим два "полярных" распределения
вероятностей: ![]() дельта-функцию
и равномерную плотность, определенную на
интервале
дельта-функцию
и равномерную плотность, определенную на
интервале ![]() . Тогда
энтропия и, соответственно, количество
информации могут принимать значения в интервале
. Тогда
энтропия и, соответственно, количество
информации могут принимать значения в интервале ![]() И если под количеством
информации понимать меру снятой
неопределенности, то можно утверждать, что
количество информации для непрерывных
распределений, может быть и отрицательным.
И если под количеством
информации понимать меру снятой
неопределенности, то можно утверждать, что
количество информации для непрерывных
распределений, может быть и отрицательным.
Найдем величину энтропии на входе и
выходе оператора ![]()
![]() (13)
(13)
где ![]() Считаем,что
в нашем случае это достаточно малая величина.
Воспользуемся формулами (10) и (11), подставляя в них
соотношения (13). Получим при
Считаем,что
в нашем случае это достаточно малая величина.
Воспользуемся формулами (10) и (11), подставляя в них
соотношения (13). Получим при ![]() и тем меньше, чем больше
и тем меньше, чем больше ![]() В этом случае
В этом случае ![]() и
тем больше, чем больше величина
и
тем больше, чем больше величина ![]() При
При ![]()
![]() и тем больше, чем меньше
и тем больше, чем меньше ![]() А величина
А величина ![]() и тем меньше, чем меньше
и тем меньше, чем меньше ![]() На наш взгляд, это и соответствует
реальной действительности. В первом случае,
когда
На наш взгляд, это и соответствует
реальной действительности. В первом случае,
когда ![]() оператор снижает
неопределенность результата, а во втором случае,
когда
оператор снижает
неопределенность результата, а во втором случае,
когда ![]() увеличивает ее.
Погрешность в
увеличивает ее.
Погрешность в ![]() при
большом значении
при
большом значении ![]() менее
значима для
менее
значима для ![]() напротив,
при малом значении
напротив,
при малом значении ![]() она
становится более значимой для
она
становится более значимой для ![]() и может стать даже соизмеримой с
и может стать даже соизмеримой с ![]() Здесь всюду под
Здесь всюду под ![]() понимается значение
переменной
понимается значение
переменной ![]() оператора
оператора ![]() как аргумент функции.
как аргумент функции.
Нетрудно представить и тот факт, что если имеем два последовательно действующих оператора
![]() (14)
(14)
то при случайных величинах ![]() описанные выше точностной
и информационный эффекты будут усиливаться.
описанные выше точностной
и информационный эффекты будут усиливаться.
3.
ПРОСТЕЙШАЯ СЛОЖНАЯ ПРОГРАММАРеальная программа достаточно сложного вычислительного процесса может быть представлена в виде графа ?(v,d,P,R), где v-множество вершин (операторов), d-множество дуг (переходов между операторами), P-множество вероятностей реализации операторов, R- множество вероятностей переходов между вершинами. При определенных значениях исходных данных на входах графа, значениях констант операторов, может существовать на графе одна и только одна траектория следования вычислительного процесса. В каждой вершине графа происходит выбор следующей вершины, к которой будет осуществляться переход процесса. Этот выбор определяется выполнением или невыполнением предикатного условия, свойственного только данной вершине. Весь процесс вычислений происходит во времени.
Провести анализ точностного и
информационного свойств для сложных программ,
описываемых подобными графами, не
представляется возможным. Поэтому рассмотрим
одну простейшую сложную гипотетическую
программу. Такая программа будет содержать ![]() однотипных линейных
операторов, рассмотренных в п.2, последовательно
реализуемых от начала процесса до его окончания.
Полагаем, что результат вычислений будет получен
только тогда, когда все
однотипных линейных
операторов, рассмотренных в п.2, последовательно
реализуемых от начала процесса до его окончания.
Полагаем, что результат вычислений будет получен
только тогда, когда все ![]() операторов
вида
операторов
вида ![]() один за другим
будут реализованы. При этом результат вычислений
предшествующего оператора является значением
входной переменной для следующего оператора.
один за другим
будут реализованы. При этом результат вычислений
предшествующего оператора является значением
входной переменной для следующего оператора.
У всех операторов коэффициенты ![]() , случайны, подчинены
одному и тому же распределению. Но при реализации
каждого элементарного оператора выбор значения
константы
, случайны, подчинены
одному и тому же распределению. Но при реализации
каждого элементарного оператора выбор значения
константы ![]() производится
заново, независимо от выбора значений ее
предшественников. Таким образом, наша задача
анализа свойства программы сводится к
суммированию ошибок всех операторов,
составляющих программу. В реальных программах
каждый элементарный оператор имеет свои
константы, по точности характеризуемые своими
распределениями.
производится
заново, независимо от выбора значений ее
предшественников. Таким образом, наша задача
анализа свойства программы сводится к
суммированию ошибок всех операторов,
составляющих программу. В реальных программах
каждый элементарный оператор имеет свои
константы, по точности характеризуемые своими
распределениями.
Однако, в подобном виде решение задачи анализа будет математически весьма громоздким. Нам же необходимо получить общие, принципиальные выводы о свойстве сложной программы.
Согласно [6 ] "вероятность того, что при сложении большого числа приближенных чисел, округленных по обычному правилу, ошибки не накапливаются, а, напротив, компенсируются", достаточно велика.
Но мы подойдем к суммированию
случайных величин опять с той же позиции, которая
предусматривает изучение плотности вероятности
суммы случайных величин, определения
вероятности ошибки при суммировании, если
пределы точности слагаемых и результата заданы.
По-прежнему полагаем, что они одинаковы и равны ![]()
Суммируя ![]() случайных
величин с плотностью вероятности (2), в
преобразовании Лапласа получаем:
случайных
величин с плотностью вероятности (2), в
преобразовании Лапласа получаем:
![]() , (15)
, (15)
![]() (16)
(16)
Из (16) найдем математическое ожидание, среднеквадратическое отклонение и коэффициент вариации выходного значения программы:
![]() (17)
(17)
где ![]() математическое
ожидание, среднеквдратическое отклонение и
коэффициент вариации константы
математическое
ожидание, среднеквдратическое отклонение и
коэффициент вариации константы ![]() отдельного оператора.
отдельного оператора.
Для аппроксимации плотности вероятности результата реализации программы воспользуемся нормальным распределением с парамиетрами (17). Найдем вероятность ошибки программы в зависимости от ее сложности:
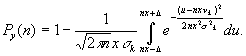 (18)
(18)
Для большей наглядности рассмотрим простой
численный, достаточно грубый пример: ![]() Получим при значениях
Получим при значениях ![]()
![]()
Несмотря на грубость примера, он достаточно наглядно поясняет сущность изучаемого вопроса, показывая как быстро растет вероятность ощибки программы в зависимости от ее сложности.
Решение задач в компьютере
производится казалось бы с весьма высокой
точностью (![]() но и это не
изменяет высказанного утверждения о росте
вероятности получения ошибочного результата от
сложности программ. Кроме того, утверждение
усугубляется и тем, что переменные задач
представляются также приближенно, приближенными
являются округления вычислений, реализации
условных переходов, которые также приводят к
накапливанию величины ошибки
но и это не
изменяет высказанного утверждения о росте
вероятности получения ошибочного результата от
сложности программ. Кроме того, утверждение
усугубляется и тем, что переменные задач
представляются также приближенно, приближенными
являются округления вычислений, реализации
условных переходов, которые также приводят к
накапливанию величины ошибки
Что касается информационных свойств программ, то они сохраняются в
основном такими же, как и у рассмотренного элементарного оператора.
4.
О ПОСТРОЕНИИ ТОЧНОСТНОЙ ТЕОРИИ НАДЕЖНОСТИ ПРОГРАММВ настоящее время основными факторами, определяющими ненадежность программного обеспечения считаются человеческий фактор, ошибки данных, программные ошибки, отказы техники [7]. Используются аналитические, статистические методы оценивания и методы моделирования. Несомненно это
очень важно и дает определенные положительные результаты для повышения надежности программного обеспечения.
Но если мы хотим защитить от ошибок программного обеспечения дорогостоящие объекты гражданского и военного назначения, необходимо уделять больше внимания аспекту точности вычислений из-за неопределенности величин их компонентов.
Классическая теория надежности технических систем использовала метод расчленения сложных объектов на элементы расчета. При этом надежность элементов рассчитывалась, в основном, с помощью справочников, в которых приводились значения интенсивностей отказов элементов. Затем оценивалась надежность объекта и принимались меры по ее повышению.
На наш взгляд, для обеспечения надежности функционирования сложных программных комплексов необходимо идти по подобному пути.
1.Определять основные простейшие операторы, из которых составляются программы.
2.Более ответственно и скурпулезно изучать точность представления различных величин операторов.
3.Исследовать точностные характеристики операторов при полученных распределениях величин.
4.Интенсивнее развивать модели исследования точностных свойств элементарных операторов.
5.Составлять справочники по результатам исследования операторов, в которых приводить инженерные рекомендации по практическому оцениванию точности операторов.
6.Разрабатывать точностные модели сложных программ на основе интегрирования элементарных операторов. Для этого можно использовать разработанные графоаналитические методы и методы моделирования.
7. При построении сложных программ из отдельных операторов необходимо производить весьма тщательное согласование выходов операторов со входами последующих операторов, а именно, областей их задания. Невыполнение этого является источником дополнительных ошибок и потерь информации[8,9].
Содержание п.7 хорошо напоминает о том, как важно согласовывать в многокаскадном электронном усилителе один каскад по выходу со входом следующего каскада. Невыполнение этого требования в граничных областях каскадов приводит к неработоспособности усилителя в казалось бы заранее предусмотренной области изменения параметров усилителя. В программах этот эффект менее очевиден, поэтому не всегда учитывается при их отладке.
5.
ЗАКЛЮЧЕНИЕОсуществление предложенного подхода к оцениванию и повышению надежности функционирования программного обеспечения требует существенных затрат различного вида. Но, на наш взгляд, его осуществление необходимо. Это обусловлено конечной точностью вычислений в современных и перспективных компьютерах и другими факторами, из которых наиболее весомым является лавинообразный рост сложности перспективных программ. Другого пути нет, пока не будут созданы компьютеры с избыточностью, позволяющей организовать оперативный контроль и принятие решений в условиях влияния помех различного вида, адаптирующиеся по точности в
процессе вычислений. Возврат к классической теории ошибок и дальнейшее ее развитие весьма необходимы в интересах информатики и информатизации общества. Такой путь, на наш взгляд, может стать источником новых конструктивных решений как в элементной базе, архитектуре вычислительных средств, так и в программном обеспечении. Он также может стимулировать развитие новых методов численной математики.В данной статье не приводятся методы исследования точности реализации различных математических операторов и примеры, иллюстрирующие значения вероятностей возникновения ошибок при реализации операторов.
СПИСОК ЛИТЕРАТУРЫ
1.Винер Н. Кибернетика, или связь в животном и машине.-Пер. с англ.-М.: Сов. радио, 1958.
2. Тейер Т., Липов М., Нельсон Э. Надежность программного обеспечения.-Пер. с англ.-М.: Мир, 1981.
3. Липаев В.В. Надежность программных средств.-М.: Синтег, 1998.
4. Тарасенко Ф.П. Введение в курс теории информации.-Томск, 1963.
5. Красовский А.А., Поспелов Г.С. Основы автоматики и технической кибернетики.-М.-Л.: Энергоатомиздат, 1962.
6. Крылов А.Н. Лекции о приближенных вычислениях.-М.: ГИТТЛ, 1954.
7. Карповский Е.Я., Чижов С.А. Надежность программной продукции.-Киев: Техника, 1990.
8. Смагин В.А. Энтропийный метод исследования информационных сетевых структур.- На сайте http://Sir35.narod.ru/, 2002.
9. Смагин В.А. Об одном источнике потерь информации.- На сайте http://Sir35.narod.ru/, 2002.
V.A. Smagin
Introduction in the accuracy theory of reliability of the software.
Key words: the software, reliability, complexity of programs,
mistake, effect of accumulation, accuracy calculations,
distribution of probabilities, modeling, the forecast.
Abstract.
V.A. Smagin. Introduction in the accuracy theory of reliability of the software.
The new approach the estimation is offered to reliability of the software, based
on the analysis of accuracy of functioning of the operators making the program
of calculations. The plan of constructions is considered and realisations of this
theory.
The bibliographies 9.
За примерами и приближенным методом
оценивания вероятности ошибок математических
операторов обращайтесь к автору статьи:
Владимир Александрович,
e-mail:
va_smagin@mail.ru,Санкт-Петербург, Россия,
тел. 7 (812) 235-27-78
![]()
.
Только подписка гарантирует Вам оперативное получение информации о новинках данного раздела
Нужное: Услуги нянь Коллекционные куклы Уборка, мытье окон