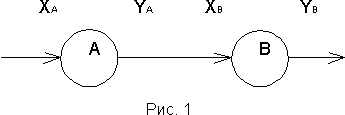
СМАГИН В.А.
Рассмотрено взаимодействие двух последовательных функциональных операторов. На основе энтропийного подхода определено количество информации, теряемой при преобразовании элементарным информационным оператором.
ОБ ОДНОМ ИСТОЧНИКЕ ПОТЕРЬ ПРЕОБРАЗОВАНИЯ ИНФОРМАЦИИ
Введение. Любой сложный процесс преобразования информации представляет собой определенную совокупность определенным образом связанных между собой элементарных функциональных операторов. В статье [1] вводится понятие энтропийной передаточной функции функционального оператора в виде отношения его выходной и входной энтропий. Приводится алгоритм определения энтропийной передаточной функции для системы преобразования информации сетевой структуры. Находится количество информации, получаемой на выходе системы. Вводится информационный передаточный коэффициент. Отметим, что приведенные в [1] результаты исследований справедливы только в том случае, когда множества значений выходных переменных предшествующих операторов полностью накрываются множествами значений входных переменных операторов, непосредственно следующих за ними. Это относится ко всем функциональным операторам, кроме первого (источника информации) и последнего (стока информации) оператора системы. Отмеченное ограничение весьма существенно и было принято для упрощения исследования.
В реальных условиях функционирования систем подобного согласования выходов и входов операторов, как правило, не наблюдается. Это может служить причиной потери некоторого количества информации в процессе ее преобразования и, как следствие, причиной появления ошибок в них. Укажем на некоторые области приложений, в которых данное обстоятельство может иметь место.
Так, например, хорошо известно насколько важно согласование различных выходов-входов современных радиоэлектронных систем. Даже обычный радиоэлектронный многокаскадный усилитель, собранный из элементов на основании теоретического расчета, как правило, не будет качественно работать до тех пор, пока отдельные его каскады не будут настроены соответствующим образом, согласованы с соседними каскадами.
.
В качестве второго примера укажем на систему “учитель-обучаемый”. Чтобы передать определенное количество знаний из некоторой области учителем обучаемому, необходимо адаптировать обе стороны друг к другу. Обучение эрудированным учителем плохо подготовленного к восприятию знаний обучаемого малоэффективно. Неэффективно и обучение эрудированного обучаемого недостаточно подготовленным учителем. Система “учитель-обучаемый” должна быть согласованной, чтобы достичь определенного, желаемого эффекта.Третья область - современные информационные и вычислительные системы. Любой алгоритм преобразования информации состоит из элементарных операторов. Эти операторы должны быть согласованы друг с другом. В противном случае может наблюдаться потеря определенного количества информации. Иначе говоря, несогласованность выходов-входов операторов может быть источником ошибок преобразования информации. Этим мы указываем на один из возможных источников ненадежного функционирования программного обеспечения современных компьютеров.
Наконец, отметим тот факт, что согласованность операторов в некоторых информационных системах не является постоянной и может изменяться во времени. Если касаться процесса информационного противодействия, то можно утверждать, что задача защиты
информации заключается в сохранении или улучшении согласованности, а задача разрушения информации - в ухудшении согласованности операторов или этапов преобразования информации.
Целью данной статьи является получение простейшей оценки количества потерянной информации в процессе взаимодействия двух функциональных операторов при ее преобразовании.
Модель взаимодействия операторов. Рассмотрим два одновходовых оператора, последовательно преобразующих информацию. На рисунке 1 показаны входы и выходы операторов А и В.
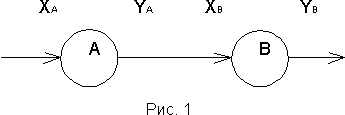
Для наглядности области задания значений входных и выходных переменных будем изображать на плоскости
. При этом потеря информации может иметь место за счет несогласования областей выходной переменной Y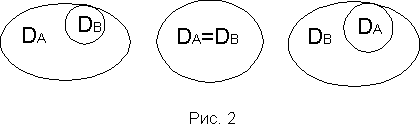
оператора A и входной переменной X
оператора B. Здесь можно наблюдать три
случая,
показанных на рисунке 2.
В первом случае оператор B может преобразовывать только часть значений выходной переменной
Y
оператора A, остальная часть значений
выходной переменной Y теряется. Во втором случае
операторы A и
B полностью
согласованы,
так как любому значению выходной переменной
оператора соответствует только одно значение
входной переменной оператора B. В третьем случае оператор B полностью
использует все возможные значения выходной
переменной оператора A. При этом не полностью
используются его возможности за счет
несогласования областей задания указанных
переменных.
Второй и третий случаи не приводят к потере
информации и нами не рассматриваются. Следует лишь отметить, что в первом и
третьем случаях могут иметь место стоимостные
потери преобразования информации за счет неполного
использования множеств значений
соответствующих переменных. Однако здесь вопрос о
стоимостных потерях нами не затрагивается.
Рассмотрим первый случай. Количество информации, получаемое на выходах операторов A и B, будет равно:
Так как информация теряется только оператором A, то количество потерянной информации будет равно:
, (1)
где 
энтропия на
выходе оператора A и энтропия на входе оператора
B. Выражение (1) можно представить в виде:
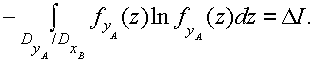(2)
Пример. Используем одномерные равномерно распределенные случайные величины. Пусть
Тогда в соответствии с [1]
(3)
Используя (2) и (3) получим
(4)
В (4) 
>1,
но 
<
В
случае, когда 
наблюдается
полное согласование выхода оператора A со входом
оператора B и потери информации отсутствуют.
Потери (4), найденные для одной и той же плотности 
и областей 
естественно
назвать безусловными потерями. Если вместо
использовать условную
плотность вероятности
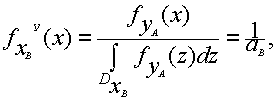(5)
то условные потери информации составят:
. (6)
Предположим, что 
.
Полное количество информации составит 
Условные потери информации составят
Спрашивается, какова
вероятность ошибиться при выполнении оператора
A?
Ее приближенно можно определить следующим образом
. Вероятность ошибки оператора A на основании геометрических соображений будет равна: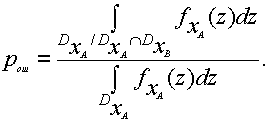
(7)
Для условий примера вероятность ошибки оператора A будет равна:
Заключение. Любой сложный информационный процесс состоит из
определенной последовательности элементарных операторов преобразования информации. Выход предшествующего элементарного оператора должен быть согласован со входом следующего за ним элементарного оператора. Это означает, что область значений выходной переменной должна накрываться областью значений входной переменной следующего оператора. Отсутствие согласования элементарных операторов является источником потери преобразования информации и как следствие источником ошибок. Предложенная в статье модель может использоваться при оценивании и повышении надежности реализации алгоритмов и программного обеспечения современных ЭВМ.
СПИСОК ЛИТЕРАТУРЫ
1.
Смагин В.А. Энтропийный метод исследования информационных сетевых структур. -Изв. ВУЗов. Приборостроение. 2001(в печати).
UDC 658.5
Smagin V.A.
On a Source of Information Transformation Losses
Interacttion is studied between two serial functional operators of the information network. On the basis of the entropy method the amount of information being lost in the process of its transformation by the elementary operator is defined. Recommendation on matching of the network operators is provided.
Ill.2, bibliogr. 1.
UZK 658.5
Smagin W.A.
Von einer Quelle der Informationswandlungverluste
Die Wechselwirkung zweier konsequenten funktio-nalen Operatoren des Informationsnetzes wird erotert. Auf dem Grunde des Entropievorgehens wird die Information-smenge, die bei ihrer Umwandlung durch den elementa-ren Operator verloren wird, bestimmt. Das Empfehlen fur die Koordinierung der Netzoperatoren wird vorgeschlagen.
Illustr.2, Bibliogr.1.
UDK 658.5
Smaguine V.A.
Consideration sur une source des pertes au cours de la transformation de l'information
On considere l'interaction de deux operateurs foctionnels en serie du reseau informationnel. Sur la base de la methode d'entropie on determine la quantite d'information perdue au cours de sa transformation par l'operateur primitif. On presente une recommendation sur l'adaptation des operateurs du reseau.
Fig.2; reference 1.
.
Только подписка гарантирует Вам оперативное получение информации о новинках данного раздела
Нужное: Услуги нянь Коллекционные куклы Уборка, мытье окон
