§ 44
При постоянстве силы,
относительная скорость 
точки прямо
пропорциональна времени действия силы
, (102)
что не противоречит идеям
Ньютона. Абсолютная скорость 
:
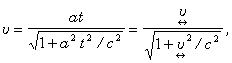(103)
что по форме не противоречит идеям Эйнштейна.
Путь, пройденный материальной точкой в равнопеременном прямолинейном движении, вычисляется по формуле:
.
Если
обратиться к 
как к конечной
скорости, то
.
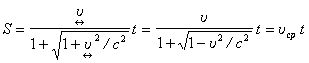(104)
Отсюда видно, что множитель
обращает конечную
относительную скорость в абсолютную скорость и придаёт ей среднее
значение 
.
Следовательно, в данном случае работа силы
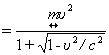, (105)
Если в правом члене
уравнения (105) скорость приравнять в величине 
, тогда получим выражение для полной энергии: 
.
Таким образом, в §35, 36 мы шли от полной энергии к работе силы. Здесь, с помощью формулы (104) мы прошли путь в обратном направлении – от работы силы к полной энергии. Для этого нам понадобились и идею Ньютона и идеи Эйнштейна, но не в раздвоенном виде, а в единстве, имеющего смысл последующей ступени в развитии физики.
2. Равномерное движение материальной точки по окружности.
§ 45
При равномерном движении по окружности, материальная точка обладает не только накопленным кинетическим стремлением, но и динамическим стремлением. Формой проявления кинетического стремления является равномерное и прямолинейное движение, а динамическое стремление - ускоренное движение. В силу этого, вектор мгновенного кинетического стремления постоянно направлен по касательной к окружности, а вектор динамического стремления – по главной нормали к центру окружности. В результате динамическое стремление искревляет
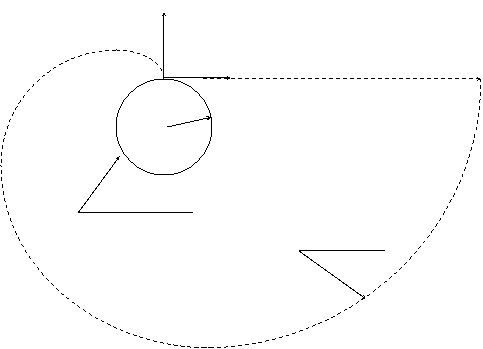
рис. 9
траекторию материальной точки, а кинетическое стремление побуждает материальную точку двигаться по искривлённой траектории равномерно. Иначе говоря, материальная точка движется по окружности одновременно и равномерно и ускоренно. Данные два явления выступают в единстве, но их можно рассмотреть и раздельно с помощью нижеследующего мысленного примера.
Свяжем центр координатной
плоскости 
, с точкой, произвольно выбранной на окружности. П материальная точка, двигаясь по окружности, в момент 
совпадает с началом
отсчета 
, а ее мгновенная скорость с осью 
положительного
направления. (рис.9). Материальная точка стремиться двигаться не только
равномерно, но и прямолинейно. В системе формой проявления
такого стремления является мнимое равномерное прямолинейное движение, радиус-вектор
которого 
. Если плоскость 
будет вращаться
вместе с материальной точкой вокруг перпендикуляра, проходящего через центр
окружности, тогда конец радиус-вектора 
в течении одного периода обращения опишет на вращающейся плоскости эвольвенту,
эволюта которой есть действительная траектория точки. Т.е. опишет траекторию
точки в мнимом равноускоренном движении, длина которой
. (106)
Если учесть, что при
движении по окружности материальная точка контактирует с такими точками
пространства, которые удалены от центра окружности на одинаковом расстоянии и
существуют одновременно, т.е. если учесть, что вращение осуществляется в
условии, когда 
, тогда величина нормального ускорения
. (107)
К концу периода обращения
скорость мнимого равноускоренного движения (скорость ‘протаскивания’ эвольвенты через конец
радиус-вектора 
)
. (108)
Следовательно, формулу (106) можно переписать в виде:
. (109)
Очевидно, раскрывая законы динамики, Ньютон базировался в основном на явлениях, происходящих во вращательном движении, и другого пути у него не было: такого была ступень в нескончаемом потоке развития истины.
