b. Еще раз о стремлении
§ 49
Все тела обладают не только центом массы, но и временной вершиной настоящего. Если тело свободное, то его центр массы и временная вершина настоящего совпадают. В этом случае существование по отношению к временной вершине настоящего неограниченно перекошено в прошлое поперечной глубины ПВК. Такой перекос называется внешним перекосом. Разъединение временной вершины тела с его центром массы осуществляется только под воздействием контактной силы. В этом случае существование по отношению к временной вершине настоящего перекашивается не в прошлое, а в будущее поперечной глубины. Такой перекос называется внутренним перекосом.
Внешние перекосы оставляют центр массы тела в прошлом поперечной глубины. Находясь в прошлом поперечной глубины, центр массы стремится к внешней временной вершине настоящего. Внутренний перекос оставляет центр массы в будущем поперечной глубины. В этом случае центр массы тела стремится к его временной вершине настоящего, а временная вершина настоящего стремясь к центру массы оказывает сопротивление контактной силе.
Стремление центра массы к внешней вершине настоящего или к внутренней вершине настоящего называется динамическим стремлением. Стремление временной вершины настоящего тела к его центру массы называется инерциальным стремлением.
Количественная мера динамического стремления называется силой динамического стремления. Количественная мера инерциального стремление называется силой инерциального стремления.
Во всех случаях суммарное значение динамического стремления есть вектор, начало которого совпадает с центом массы тела. Следовательно, центр массы тела выступает не только как центр инерции, но и как побудительный центр.
Примечание. Дополнительно к вышеизложенному предлагается следующая рабочая схема: помимо гравитационного и инерциального полей в природе существуют и другие поля, но в любом случае, это есть перекошенное пространство, в каждой точке которого соответствующие полю волны вызывают у помещённой туда частицы динамическое стремление. Следовательно, там, где по существующим взглядам усматриваются ‘силы притяжения’ или ‘силы отталкивания’, там следует учитывать перекосы в существовании, устремлённые соответствующим образом или в прошлое, или в будущее поперечной глубины ПВК. По-видимому, каждый атом имеет свой собственный центр массы, свою собственную временную вершину настоящего и определённое количество временных оболочек настоящего, к которым тяготеют электроны. При этом внешняя временная оболочка образует поверхность атома, а внешние временные оболочки внешних атомов образуют поверхность молекулы и тела. Иначе говоря, каждый атом обладает сложной временной структурой, являющаяся устойчивой основой для его существования.
c. Сила динамического
стремления при движении
планеты по круговой орбите
§ 50
В системе отсчёта, построенной на базе центра массы солнечной системы, продольное пространство, по отношению к временной вершине настоящего равномерно и неограниченно перекошено в прошлое поперечной глубины. Перекошенное пространство называется гравитационным полем. Гравитационное пол допускает распространение гравитационных волн, вызывает у планеты динамическое стремление, вектор которого направлен от центра массы планеты вдоль образующей конического перекоса к временной вершине настоящего солнечной системы.
Количественная мера проявляемого планетой динамического стремления, называется силой динамического стремления или гравитационной силой и согласно закону динамики определяется по формуле:
, (112)
где 
- масса планеты,
характеризующая тенденцию динамического стремления к устойчивости; 
нормальное ускорение,
характеризующее тенденцию динамического стремления к изменчивости. А если это
так, тогда равенство (111) можно переписать в виде
, (113)
где 
- масса солнечной
системы.
Теперь воспользуемся
третьим законом Кеплера и перемножим все члены равенства (131) на 
и мы получим формулы,
характеризующие гравитационный параметр 
:
. (114)
Отсюда видно, что гравитационный параметр это величина тенденции к изменчивости на единичном расстоянии от центра тяготения.
Однако, планета обладает не только динамическим стремлением, но и накопленным кинетическим стремлением. При круговой орбите их векторы постоянно направлены друг к другу перпендикулярно, что позволяет кинетическому стремлению разворачивать вектор динамического стремления, а динамическому стремлению разворачивать вектор кинетического стремления. В результате планета, падая, свободно движется вокруг центра массы солнечной системы.
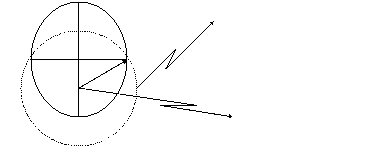
рис. 10
То, что планета обращается вокруг Солнца не по круговой, а по эллиптической
орбите, от этого суть равенства (114) не меняется и вот почему. Каждая
эллиптическая орбита имеет свою собственную мнимую круговую орбиту (на рис.10
обозначена пунктиром), которая находится с нею в одной плоскости и пересекаются
в точках. 
и 
. Известно, что периоды обращения планеты по эллиптической орбите и по мнимой
круговой орбите одинаковые (
). Кроме того, соблюдаются и такие одинаковости как 
(
- большая полуось эллиптической орбиты), а в точках и - тенденций к
изменчивости и количеств накопленного кинетического стремления. Следовательно,
гравитационный параметр (114) и постоянная
Гаусса имеют не только одинаковые значения, но и одинаковый смысл:
, (115)
где 
- радиус мнимой
круговой орбиты, 
- большая полуось эллиптической орбиты.
