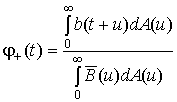 , (1)
, (1)Смагин В.А.
Оптимальное квантование информации в условиях противодействия
Представлено выражение для вероятности успешной передачи квантованной информации в условиях противодействия. Выполнен его анализа с учётом влияния различных факторов.
Введение. Под информацией понимаются различные сведения, представимые в количественном виде. Такими сведениями могут быть сведения, приводимые в книге, передаваемые с помощью средств различной физической природы, записываемые на носители для хранения, считываемые из хранилищ, представимые словесно и т.д.
Любая информация, представимая количественно, может сравниваться с другой количественно эквивалентной информацией. В качестве такого признака сравнения информации может выступать её ценность. Количество информации и её ценность изучались в научно-технической литературе [1,2] и других источниках. Однако, несмотря на их вероятностный смысл в процессе многих системных аналитических исследований оба указанных параметра, как правило, не представлялись случайными величинами, характеризуемыми определёнными вероятностными распределениями.
Достаточно общим свойством, присущим практически любому виду информации, является её квантованность, т.е. представление в виде определённых конечных величин. Кванты информации, как правило, представляются не случайными величинами (количеством бит, слов и т.д.).
В последнее время в связи с развитием теории информационной борьбы, теории информационного конфликта и информационного противоборства, интерес исследователей к квантовому представлению информации должен увеличиваться. Во-первых, квантовое представление информации объективно существует в природе, технике, экономике и обществе. Во-вторых,
главным образом, на основе квантового представления информации могут наиболее полно отражаться в исследованиях процессы как информационного взаимодействия, так и информационного противоборства различных сторон и систем.В данной статье изучается вопрос квантового информационного взаимодействия двух сторон. Одна из этих сторон представлена как система передачи информации от источника к получателю (стоку). Она стремится реализовать в процессе своего функционирования некоторое количество информации. Другая сторона (противник, мешающий фактор) стремится снизить, уменьшить количество информации, передаваемой первой стороной. Передача информации первой стороной осуществляется квантами, разделёнными некоторыми паузами. Отличительной особенностью статьи является то
, что квант передаваемой информации и для искажаемой противником в кванте информации рассматриваются как случайные величины, заданные своими распределениями вероятностей. Неслучайное квантование информации рассматривалось в [3], а случайное – в [4]. Однако вероятностное неслучайное квантование в условиях противодействия одной из сторон здесь рассматривается впервые. Отметим, что мы ограничиваемся получением количественных соотношений, не привлекая понятия ценности информации. Это объясняется тем, что представить в вероятностном виде ценность информации мы пока не можем. Представление ценности информации в форме, указанной в [2] и связанной с характеристикой стоимости, является весьма ограничительным. Представление ценности информации в вероятностном виде [5] является весьма интересным, хотя оно и относится к музыке. Однако воспользоваться им в техническом, системном аспекте достаточно затруднительно. Иначе говоря, описание ценности как случайной величины с соответствующим распределением вероятностей, на наш взгляд, актуально, но требует дальнейшего изучения.Вероятность успешного сообщения квантованной информации. Пусть
t есть длительность кванта информации, передаваемого первой стороной. Она случайна и характеризуется функцией распределения длительности кванта B(t). Обозначим через A(t) функцию распределения длительности кванта информации, искажаемой противником в процессе передачи кванта информации первой стороной. Обе функции распределены на положительной полуоси [0,Ґ ). Тогда плотность вероятности длительности кванта неискажённой информации, найденная для разности двух случайных величин, будет равна: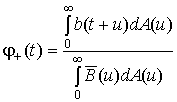 , (1)
, (1)
где:
j+(t) – условная плотность вероятности длительности кванта, определённая на положительной полуоси [0,Ґ ), что соответствует случаю неполного искажения кванта информации внешним воздействием; b(t) = Bў (t),Вероятность того, что длительность кванта неискажённой информации будет не менее
t, равна: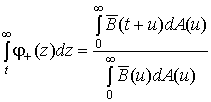 . (2)
. (2)
Из выражения (2) легко видеть, что данная вероятность монотонно убывает, может изменяться от 1 при
t = 0 до 0 при t ® Ґ , что соответствует реальной действительности.Предположим, что полное количество передаваемой информации (длительность передачи) случайно и распределено с функцией
Y(z), z[0,Ґ ). Кванты информации, передаваемой к получателю, разделяются паузами, длительность паузы равна с, а вероятность реализации паузы равнаЕсли длительность кванта равна
t, а полное количество информации – z, то число квантов, необходимых для передачи, определяется как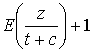 ,
,
где Е
(х) – наименьшая целая часть х.Учитывая случайность входящих в последнее выражение величин и принимая указанные выше вероятности их осуществления получим вероятность передачи полного количества информации в неискажённом виде
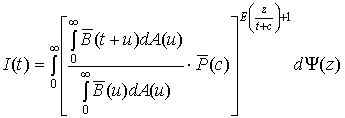 . (3)
. (3)
Это и есть основное выражение для вероятности успешного сообщения полного количества квантованной информации, передаваемой квантами длины
t с разделяющими их паузами длины с.Анализ основного выражения. В общем случае, при произвольных распределениях
B(t), A(t), P(c), Y(z), выполнить анализ (3) не численными методами, в замкнутом виде, не представляется возможным. Рассмотрим лишь один частный случай. Предположим, что B(t) – произвольное распределение, Аў (х) = =d(x – X0), Yў (х) = =d(z – Z0), где d - дельта-функция Дирака. Тогда из (3) следует: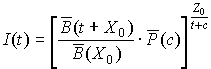 . (4)
. (4)
В (4) принято ![]() .
Дифференцируя (4) по
.
Дифференцируя (4) по
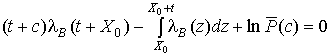 , (5)
, (5)
где ![]()
Аналогичным образом из (4) можно найти и оптимальную длительность паузы с
0, которая может быть определена из уравнения: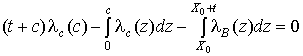 , (6)
, (6)
в котором ![]()
Интересно отметить, что если потребовать, чтобы
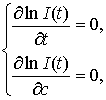 (7)
(7)
то есть выражения (5) и (6) выполнялись совместно, тогда можно получить
l
B(t0+X0) = lc(c0). (8)Из (8) можно найти при известных
lB, lc явную зависимость длины кванта t0 от длины паузы с0.Рассмотренный частный случай решения приведён для иллюстрации возможности решения (4) в замкнутом виде. Он соответствует ситуации, когда квант искажённой информации х и полная длина сообщения
z не случайны.Максимальное значение
I(t) находится в результате подстановки в (4) значений t0, с0 или одновременно t0 и с0. В общем случае (4) следует решать численными методами.Пример численного решения. Пусть осуществляется передача заданного количества информации от источника к получателю, представленная квантами и паузами между ними. Источник помех может уменьшить количество полезной информации в кванте передачи. Известны следующие исходные данные. Законы распределения
B(х), A(х), P(х), Y(х) – нормальные. Значения их параметров соответственно равны:тВ
= 7, тА = 0,5, тР = 1, тY = 20,пВ
= 1,5, пА = 0,1, пР = 0,2, пY = 3,где т
, п – математическое ожидание и среднеквадратическое отклонение соответствующих случайных величин – параметров указанных четырёх распределений вероятностей. Для простоты анализа полагаем, что нормирующие коэффициенты всех плотностей вероятностей равны единице. Величина паузы принята с = 1.В результате численного решения на ПЭВМ выражения (3) при этих исходных данных получена кривая вероятности успешной передачи полного количества информации, представленная на рис.1.
Из данного рисунка следует, что при указанных исходных данных примера, оптимальная длина передаваемого кванта информации от источника к получателю
t0 » 1,8. Ей соответствует максимальное значение вероятности успешной передачи полного количества информации, заданного распределением Y(x), равное I(t0) » 0,96. Решение данного примера на ПЭВМ Пентиум ММХ в среде Mathcad 8 требует около часа времени.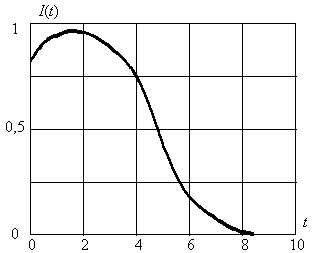
Рис.1
Пример выбора стратегий противоборствующих сторон. В данном примере рассмотрим простейшую игровую схему взаимодействия двух сторон. Первую противоборствующую сторону представляет источник – приёмник информации. Вторую сторону – источник помех. Каждая из названных сторон располагает двумя возможными стратегиями своего поведения. Каждой стратегии соответствует свой набор численных значений параметров распределений. Распределения полагаются нормальными. Длительность кванта для первой стороны (А) определяется параметрами:
стратегия А
1 – тВ = 13, пВ = 4; стратегия А2 – тВ = 15, пВ = 4.Для второй стороны (В) длительность кванта разрушения информации определяется параметрами:
стратегия В
1 – тА = 2, пА = 0,5; стратегия В2 – тА = 4, пА = 0,5.Длительность паузы между квантами принята с = 1, а вероятность её реализации подчиняется нормальному закону распределения с параметрами тР
=2, пР = 0,5. Вероятность осуществления паузы будет равнаВ результате численного решения (3) для данных стратегий сторон получим следующую таблицу вероятностей успешной передачи полного количества информации от источника к получателю (т
Y = 20, nY =3)*.Таблица 1
А В |
А 1 |
А 2 |
В 1 |
0,72 t0 = 3,4 |
0,61 t0 = 2,2 |
В 2 |
0,79 t0 = 4,5 |
0,70 t0 = 3,5 |
Из анализа данной таблицы следует, что в рассматриваемой игровой ситуации существует седловая точка [6] со значением
I(t0) = 0,70. Поэтому каждая из сторон может воспользоваться только одной из своих чистых стратегий. Такими стратегиями являются: стратегия А2 для стороны А и стратегия В2 для стороны В. В таблице также указана величина оптимального кванта информации для стороны А, позволяющая достичь максимума вероятности I(t0). Данный пример лишь иллюстрирует одну из возможностей использования предложенного подхода для принятия решения в конкретной неопределённой ситуации.Выражение (3) может быть использовано в других прикладных задачах. В частности, например, противодействующая сторона может изменять продолжительность паузы. Следует также отметить, что здесь мы рассмотрели аддитивный подход при формировании кванта полезной информации. Может быть рассмотрен также и мультипликативный подход при формировании кванта. И, конечно, несомненный интерес представляет решение задачи квантования информации с учётом введения функций распределения её ценности. По-видимому, здесь следует указать на одну из интересных работ [7], в которой рассматривается новый подход к понятию ценности информации.
СПИСОК литературы
![]()
.
Только подписка гарантирует Вам оперативное получение информации о новинках данного раздела
Нужное: Услуги нянь Коллекционные куклы Уборка, мытье окон