![]() УДК 519.2
УДК 519.2
Дуалистический принцип теории случайных
процессов
Построено распределение вероятностей обратной случайной величины времени наступления события. Дано его аппроксимационное представление. Изложены соображения по использованию в инженерных приложениях.
Введение. В теории надежности, массового обслуживания, эффективности и др. нашли широкое распространение распределения вероятностей случайной величины времени наступления некоторого события. Это, например, время до отказа технической системы, время работы вычислительного устройства до ошибки в нем, время восстановления работоспособности системы, время до наступления заявки в системе массового обслуживания, время обслуживания заявки в ней, продолжительность выполнения операции и т.д. При этом для оценивания любого свойства систем как правило используется не один показатель, а некоторая их совокупность. Это оправдывается тем, что ни один показатель не может достаточно полно характеризовать изучаемое свойство системы. При производстве расчетов показателей сложных систем, состоящих из отдельных элементов, значимость известных показателей в силу ряда причин также различна. Выбор необходимых показателей определяется рядом факторов (длительностью работы, избыточностью, восстанавливаемостью, темпом обслуживания, скорострельностью и др.) функционирования системы [1,2]. Введение новых дополнительных показателей, отражающих неизвестные частные компоненты целого, интегрального свойства системы в ряде случаев может быть необходимым и достаточно результативным.
Дуалистический принцип теории случайных процессов означает двойственность (дуальность) подхода в изучении случайных событий, явлений. Он позволяет наряду с временными распределениями использование скоростных распределений вероятностей в исследованиях случайных процессов.
В статье [3] на основании изучения свойств рекуррентных случайных процессов восстановления предложено построение скоростного (фидуциального) распределения вероятностей случайных событий. Приведены варианты использования его в задачах оценивания продуктивности (производительности, пропускной способности) сложных систем. Отмечены преимущества применения подобных распределений при изучении систем, характеризующихся показателем “скорость производства продукции”.
В данной статье, являющейся дальнейшим развитием дуалистического принципа, сделана попытка построения скоростного распределения для систем, характеризуемых однократными случайными событиями, без рассмотрения потоков случайных событий во времени. Статья завершается рекомендациями по практическому использованию дуалистического принципа в исследованиях систем.
Основные соотношения. Предположим,
что время до наступления некоторого события есть
случайная величина ![]() ,
подчиненная распределению
,
подчиненная распределению ![]() . Рассмотрим величину
. Рассмотрим величину ![]() . Она имеет смысл скорости наступления
единичного события. Найдем ее распределение
вероятностей
. Она имеет смысл скорости наступления
единичного события. Найдем ее распределение
вероятностей![]() .
Предполагаем, что обе случайные величины
положительны, непрерывны и существуют их
плотности вероятностей
.
Предполагаем, что обе случайные величины
положительны, непрерывны и существуют их
плотности вероятностей ![]() .Тогда
в соответствии с [4] имеем:
.Тогда
в соответствии с [4] имеем:
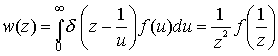 ,
(1)
,
(1)
где ![]() - дельта
– функция Дирака. Соответствующая (1) функция
распределения равна
- дельта
– функция Дирака. Соответствующая (1) функция
распределения равна
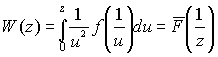 ,
(2)
,
(2)
а дополнительная функция (надежности) имеет вид
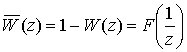 ,
(3)
,
(3)
где ![]()
Интенсивность наступления события определяется формулой [1]
![]()
![]() .
(4)
.
(4)
Введем соответствующее выражение для скоростной интенсивности наступления события
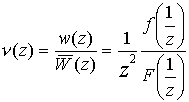 .
(5)
.
(5)
Из формулы (4) получают
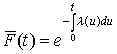
- известное в теории случайных процессов выражение.
Аналогично ему можно записать формулу
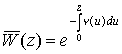 ,
,
подставляя в которую (5), после простого преобразования получим (3), что и следовало ожидать.
Преобразование Лапласа плотности распределения (1) равно
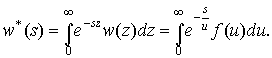 (6)
(6)
Справедливо также и соотношение
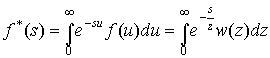 , (7)
, (7)
где ![]() - символ
изображения и переменная Лапласа.
- символ
изображения и переменная Лапласа.
Из выражений (6) и (7) дифференцированием по
s, полагая s=0, нетрудно убедиться, что в областиПримеры скоростных распределений. В качестве примеров рассмотрим скоростные распределения для экспоненциального, равномерного и усеченно-нормального временных распределений.
Экспоненциальное распределение.
![]() .
.
Для соответствующего скоростного распределения получим:
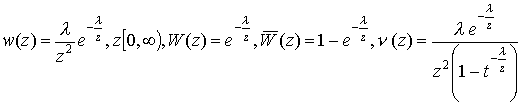 .
.
Равномерное распределение.
![]() .
.
Для скоростного распределения имеем:
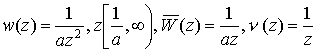 .
.
Усеченно-нормальное распределение.
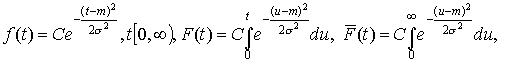
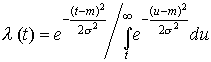 .
.
Для скоростного распределения
получим: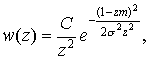
С - постоянная величина. На рисунках приведены
графики показателей скоростного распределения.
По оси абсцисс отложена величина z , размерность
которой равна час![]()
<Господа! Редакция сайта приносит свои извинения за свою безграмотность. Попытка перенести графики из формата doc в формат html у нас не получилась. Если они Вам требуются, пришлите свой email, мы Вам их персонально пришлем в
формате doc. СИРИН.>
Аппроксимационное представление. В прикладном анализе случайных процессов представляет определенные вычислительные преимущества использование гипердельтного распределения [5]. Поэтому рассмотрим сначала вырожденное временное распределение, плотность вероятностей которого равна:
![]() (8)
(8)
где Т – временной параметр распределения. Соответствующая плотность скоростного распределения имеет вид:
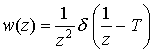 .
(9)
.
(9)
Из [5] следует, что произвольную плотность распределения, имеющую конечные начальные момента, можно приближенно представить в виде:
![]() (10)
(10)
где ![]() -
вероятности, удовлетворяющие условию
-
вероятности, удовлетворяющие условию 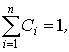 а
а
F (t) (11)
в которой ![]()
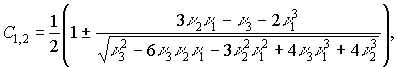 (12)
(12)
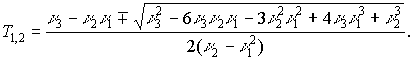 (13)
(13)
Значения постоянных
Ti, Ci найденные по формулам (12), (13) для некоторых распределений, приведены в [5].Представление плотности временного распределения в виде (10) позволяет найти аппроксимацию плотности соответствующего скоростного распределения
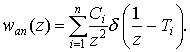 (14)
(14)
В этом случае начальные моменты случайной величины скорости наступления события будут конечными и равными
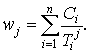 (15)
(15)
Рассмотрим алгоритм построения плотности скоростного распределения с использованием формулы (7). Представим ее в виде
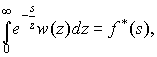 (16)
(16)
а плотность
w(z) – суммой двух d -функций![]()
![]() (17)
(17)
Подставляя (17) в (16) получим
![]() (18)
(18)
Применив метод моментов из (18) получим систему уравнений
![]()
где ![]() -
начальные моменты временного распределения,
-
начальные моменты временного распределения,
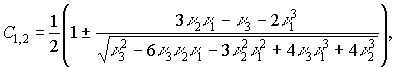 (19)
(19)
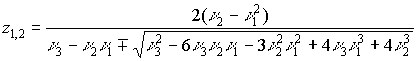 .
(20)
.
(20)
Рассмотрим пример. Пусть 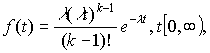 то есть плотность временного
распределения есть гамма – плотность. Применив
(19) и (20), найдем значения коэффициентов
то есть плотность временного
распределения есть гамма – плотность. Применив
(19) и (20), найдем значения коэффициентов
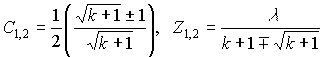 (21)
(21)
и подставляя их в (17), получим искомую плотность.
Аналогично определяется плотность скоростного распределения для любого временного распределения.
Для отыскания плотности временного распределения необходимо по известному скоростному распределению применить этот же алгоритм, но вместо формулы (7) использовать формулу (6).
Применение дуалистического принципа в исследованиях.
Надежность. а) Неизбыточная система с основным соединением двух элементов. Вероятность безотказной работы данной системы равна
![]() (22)
(22)
Заменяя в (16) выражения для ![]() согласно (2) получим
согласно (2) получим
(23)
Согласно данному выражению переход от временных к скоростным распределениям приводит к определению функции распределения скорости наступления события в виде произведения функций распределения скоростей элементов.
б) Избыточная (резервированная) система с параллельным соединением элементов. Отказ системы наступает при отказе обоих элементов.
Вероятность отказа системы равна
![]() (24)
(24)
Применяя к (24) соотношение (3) будем иметь
![]() ,
(25)
,
(25)
согласно которому вероятность того,
что скорость наступления отказа системы будет не
менее ![]() , равна
произведению соответствующих вероятностей
элементов.
, равна
произведению соответствующих вероятностей
элементов.
Выражения (23), (25) отражают дуалистический принцип для обеих систем со скоростными распределениями по отношению к выражениям (22), (24), для этих же систем с временными распределениями. Справедливо и обратное.
Производительность. а) Система с
последовательными узлами обслуживания. Для
системы из двух узлов вероятность того, что
скорость обслуживания будет не менее ![]() , равна
, равна
![]() (26)
(26)
Применяя к (26) соотношение (3), будем иметь
![]() ,
(27)
,
(27)
где ![]() - функция
распределения длительности до наступления
события.
- функция
распределения длительности до наступления
события.
б) Система с параллельными источниками. Наблюдаем здесь случай суммирования скоростей независимых друг с другом источников. Плотность вероятности величины суммарной скорости равна
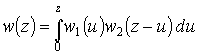 ,
(28)
,
(28)
где ![]() -
плотности распределений скоростей источников.
Применяя к (28) соотношения (1) и (6), получаем
уравнение
-
плотности распределений скоростей источников.
Применяя к (28) соотношения (1) и (6), получаем
уравнение
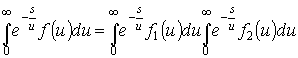 ,
(29)
,
(29)
которое необходимо решить
относительно ![]() . Или, во
временной области
. Или, во
временной области
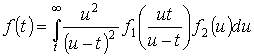 .
(30)
.
(30)
Формулы (26) и (27), (28) и (30) отражают дуалистический принцип данных систем относительно скоростных и временных распределений.
При исследовании производительности
(продуктивности, пропускной способности и т.д.)
систем, они позволяют переходить от скоростных к
временным или от временных к скоростным
распределениям, когда это необходимо. Однако, с
вычислительной точки зрения, такой переход во
многих случаях становится достаточно
трудоемким. Например, чтобы найти ![]() из (29), необходимо при известной
правой части, представленной в комплексной
форме, когда
из (29), необходимо при известной
правой части, представленной в комплексной
форме, когда ![]() и
и ![]() известны, решить
уравнение типа Фредгольма первого рода
относительно искомой функции
известны, решить
уравнение типа Фредгольма первого рода
относительно искомой функции ![]()
Рассмотрим простейший пример
отыскания ![]() по известным
по известным ![]()
![]() ,
,
откуда находим 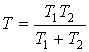 . Поэтому искомая плотность будет равна
. Поэтому искомая плотность будет равна
![]()
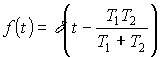 .
.
Данный пример носит иллюстративный
характер. В более общем случае, когда ![]() и
и ![]() представлены суперпозициями (суммами)
дельта-функций, отыскание
представлены суперпозициями (суммами)
дельта-функций, отыскание ![]() в виде суперпозиции становится достаточно
сложным.
в виде суперпозиции становится достаточно
сложным.
Рассмотрим более сложный пример.
Имеется двухфазная система обслуживания
(последовательные фазы). В каждой фазе содержится
![]() и
и ![]() соответственно одинаковых источников
обслуживания заявок. Требуется определить
плотность распределения скорости обслуживания
заявок системой, если плотности распределения
скоростей источников в фазах известны. Они могут
быть найдены по временным распределениям.
соответственно одинаковых источников
обслуживания заявок. Требуется определить
плотность распределения скорости обслуживания
заявок системой, если плотности распределения
скоростей источников в фазах известны. Они могут
быть найдены по временным распределениям.
На основании (26) имеем
![]() ,
,
где ![]() -
вероятности того, что величина скорости системы
и фаз будет не менее
-
вероятности того, что величина скорости системы
и фаз будет не менее ![]() .
Используя (22) и преобразование Лапласа, найдем
.
Используя (22) и преобразование Лапласа, найдем
![]() ,
,
где ![]() -
изображения плотности распределения
-
изображения плотности распределения
![]() ,
,
откуда и найдем изображение плотности
распределения системы. Окончательно, переходя от
изображения к оригиналу ![]() , находим искомую плотность распределения
скорости обслуживания системы. Отметим, что
решение указанной задачи во временной области
непосредственно более затруднительно.
, находим искомую плотность распределения
скорости обслуживания системы. Отметим, что
решение указанной задачи во временной области
непосредственно более затруднительно.
Рассмотренную задачу оценивания
производительности называют прямой. Обратной
задачей к ней называют задачу синтеза
максимальной (или заданной) производительности
при наличии некоторых ограничений. Например,
пусть требуется обеспечить максимум ![]() при условии, что на
систему наложено ограничение
при условии, что на
систему наложено ограничение
![]() ,
,
где ![]() -
ограничительные характеристики отдельных
источников фаз. Тогда имея аналитическое
выражение для
-
ограничительные характеристики отдельных
источников фаз. Тогда имея аналитическое
выражение для ![]() необходимо
найти
необходимо
найти ![]() - количества
источников фаз, обеспечивающие максимум
- количества
источников фаз, обеспечивающие максимум ![]()
Внутри данного примера рассмотрим частный иллюстрационный пример. Пусть плотности скоростных распределений фаз равны
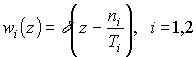 .
.
Тогда необходимо решить задачу
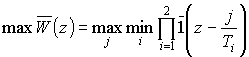 ,
,
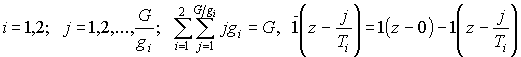 .
.
Здесь ![]() -
единичная и единичная дополнительная функции. В
качестве начального приближения можно взять
количества
-
единичная и единичная дополнительная функции. В
качестве начального приближения можно взять
количества
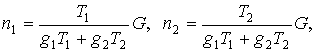
которые получаются из условий
Решение подобных задач представляет самостоятельную проблему, выходящую за рамки статьи.
СПИСОК ЛИТЕРАТУРЫ
![]()
.
Только подписка гарантирует Вам оперативное получение информации о новинках данного раздела
Нужное: Услуги нянь Коллекционные куклы Уборка, мытье окон