. (1)
СМАГИН В.А., академик МАИ
Предложен принцип получения данных о надёжности функционирования программного обеспечения на основе форсирования быстродействия персональных ЭВМ.
Введение
. В настоящее время в самых различных сферах народного хозяйства, военного дела и других отраслях человеческой деятельности получили широкое применение персональные ЭВМ (ПЭВМ). Сложность их программного обеспечения (ПО) достигла значительных величин. В дальнейшем будет наблюдаться её всё более прогрессирующий рост [1].В работе [2] отмечается: “в мире постоянно происходят катастрофы, большие и малые аварии и всё чаще их причиной становится ненадёжное функционирование компьютерных систем, и в частности, их программного обеспечения. оборона, авиация и космос, медицина, технологические процессы на современных ядерных, химических и других производствах – вот неполный перечень тех предметных областей, где низкое качество ПО и даже единичные дефекты в нём находят воплощение в терминах человеческих жизней и разрушенных материальных ценностей”. Над подобными “ответственными” системами работает целая отрасль с огромными денежными затратами, располагающая значительным количеством высококвалифицированных программистов и проектировщиков, хорошо поставлен меджемент, отлажены процессы разработки, испытаний и контроля. И тем не менее ПО даёт порой такой сбой, резонанс от которого бывает весьма громким [2].
Основными причинами проявления ошибок ПО являются недостаточно высокий уровень технологии производства программных средств и их чрезмерная сложность. И несмотря на то, что в области качества и надёжности программных средств за последнее время достигнуты определённые положительные результаты и ошибки в процессе функционирования ПО сравнительно редки, проблема обеспечения высокой надёжности сложного ПО остаётся достаточно злободневной. Для решения данной проблемы нужен комплексный, системный подход. Конечно, охватить все стороны данной проблемы в отдельной статье невозможно. Здесь мы только наметим подход к получению количественных оценок надёжности ПО на основе известного, традиционного принципа теории надёжности технических систем - принципа ускоренных испытаний.
Причина обращения к данному принципу в теории надёжности техники и ПО одна и та же. Современная теория оперирует с численными оценками. Хорошо известно парадоксальное противоречие: чем более надёжный продукт мы создаём, тем труднее оценить и подтвердить его надёжность. Однако на практике эту задачу как-то необходимо решать, чтобы при реализации системой цели можно было принять правильное решение. Сжатие информации об ошибках системы во времени в данном случае есть единственный выход из ситуации, когда в процессе её испытаний в реальном времени может не хватить ни времени испытаний, ни ресурсных затрат, или, в крайнем случае, сама система может морально устареть.
Применительно к ПО следует различать две разновидности ускоренных испытаний. К первой отнесём испытания ПО на средствах вычислительной техники (СВТ), работающих в реальном масштабе времени. Сжатие информации об ошибках здесь достигается либо более интенсивной загрузкой задачами СВТ, либо преднамеренным сокращением ресурсных возможностей СВТ определённой архитектуры [3]. В этом случае по сравнению со штатным режимом эксплуатации СВТ ставятся в более тяжёлые условия, приводящие к возникновению дополнительных “нерасчётных” ошибок. Далее, на основе некоторых моделей, например моделей подобия процессов, эти ошибки переносятся или пересчитываются в условия штатного режима эксплуатации.
Вторая разновидность ускоренных испытаний – форсированные испытания. Сущность их сводится к следующему. Программы, составленные для СВТ, функционирование которых должно происходить в реальном времени и штатных технических условиях, подвергаются ускоренному прогону на СВТ. Это достигается увеличением
тактовой частоты ячеек чипов за счёт увеличения частоты работы кварцевых генераторов тактовых импульсов ПЭВМ. Ячейки логических элементов, работая вблизи границ областей устойчивости, чаще ошибаются, чем в нормальных условиях. На “ненадёжное поле” ячеек компьютера накладывается процесс вычислений, траектория которого определяется алгоритмом программы, которой в силу ряда причин присущи свои потенциальные ошибки. Эти потенциальные ошибки в неустойчивой среде проявляются интенсивнее, чем в обычных условиях. Конечно, проявившиеся ошибки будут определяться и техническими и программными дефектами. Но это соответствует реальным процессам вычислений на СВТ. Отделить причину возникшей ошибки одну от другой часто не предоставляется возможным – в ней “виноват компьютер”. Пользователю нужен правильный результат. Поэтому, на наш взгляд, подобное форсирование одновременно работы структуры СВТ и её программы целесообразно* .Первая разновидность ускоренных испытаний, на наш взгляд, наиболее предпочтительна для испытаний системного ПО, которое мы понимаем как учёт внешней среды – системы в целом, влияния её интерфейса, человека-оператора и др. факторов.
Вторая разновидность ускоренных испытаний наиболее целесообразна для вычислительных алгоритмов типовых задач.
И, наконец, более сложными испытаниями ПО являются испытания при совмещении обеих разновидностей.
В данной статье делает упор на обсуждение форсированных быстродействием испытаний ПО.
Элементарная модель для коэффициента ускорения. Целью форсированных испытаний ПО является ускоренное обнаружение и устранение ошибок или повышение надёжности ПО благодаря процессу тестирования его на СВТ, обладающих большим быстродействием (производительностью) по сравнению с быстродействием (производительностью) штатных вычислительных средств, для которых оно предназначено. Конечно, вычислительный процесс в обоих случаях будет различным. Но в определённых пределах подобия оба процесса вычислений могут быть адекватными. Это утверждение требует и дальнейшего изучения, и экспериментальной проверки.
Предположим, что длительность тестирования некоторого ПО на штатном СВТ с быстродействием В
0 равна t0 единиц времени. Вероятность ошибки на одну команду в СВТ с быстродействием В положим равной b(B)=b0+a(B–B0)m, где b0 – вероятность ошибки на одну команду в СВТ с быстродействием В0, a - коэффициент пропорциональности вероятности ошибки быстродействию СВТ, т – степенной коэффициент. В – есть быстродействие технологического (испытательного) СВТ. Спрашивается, каково должно быть время тестирования ПО tT на технологическом СВТ с быстродействием B> B0, чтобы вероятность отсутствия ошибки на штатном СВТ за время t0 была бы равна вероятности отсутствия ошибки на технологическом СВТ?Считая вероятность ошибки на одну команду малой величиной, запишем выражение для вероятности отсутствия ошибки ПО за время испытаний на технологическом СВТ [4]:
. (1)
Вероятность отсутствия ошибки на штатном СВТ за время испытаний
t0 будет равна:
. (2)
Приравнивая (1) и (2), находим:
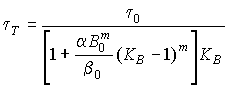, (3)
где К = В
/В0 – коэффициент форсирования быстродействия СВТ.Рассмотрим пример. Пусть
b0 = 10–4, a = 10–10 с/оп., В0 = 105 оп/с, В = 106 оп/с, т = 1. Тогда из (3) получим tT » t0/100. Если т = 1,1, тогда tT » t0/140. Данный пример показывает реальную возможность реализации процесса форсированного тестирования ПО на технологическом СВТ для обнаружения и устранения ошибок.Приведённая модель и пример носят гипотетический характер. В реальных условиях модель пересчёта времени (3) должна строиться с учётом конкретных особенностей структуры ПО, штатного и технологического средств.
Структура испытательного стенда. Стенд должен содержать следующие основные компоненты. Прежде всего его элементом является технологическая ПЭВМ. Данная ПЭВМ должна иметь возможность изменять в достаточно широком диапазоне частоту задающего генератора тактовых импульсов, захватывая область неустойчивой работы. Частота может изменяться оператором непрерывно или дискретно. Практически легче реализовать дискретное изменение частоты с помощью встроенного переключателя.
Загрузка ядра – технологической ПЭВМ – должна производиться типовыми программами автоматически последовательно после завершения предшествующих программ или фиксации их прерываний из-за обнаруженных ошибок. Этот процесс следует осуществлять с помощью управляющей ПЭВМ, снабжённой соответствующим программным управлением.
Третьим элементом стенда является программный или аппаратно–программный контроль состояния функционирующей программы. При этом нужно осуществлять контроль окончания выполнения программы и правильности полученного результата или контроль процесса срыва нормального её функционирования.
Четвёртый элемент стенда служит для накопления числа выполненных на ПЭВМ прогонов и числа срывов программ. Им же осуществляется и математическая обработка полученных статистических данных о над1ёжности ПО в результате форсированных испытаний.
Пересчёт результатов форсированных испытаний к нормальным условиям
.а) Стационарный процесс Пуассона. Статистические данные об ошибках отражают вклад или влияние различных факторов (исходных данных, аппаратурной неустойчивости, собственных ошибок ПО и др.). Поэтому модель в интегрированном виде должна отражать влияние комплекса воздействующих факторов. В силу редкости возникновения ошибок (даже при сильном ужесточении быстродействия ПЭВМ) можно полагать справедливым применение закона Пуассона, согласно которому для стационарного случайного процесса вероятность появления
k ошибок на интервале времени t будет равна:
, (4)
где
l - интенсивность ошибки при функционировании ПО в некотором произвольном режиме и в предположении, что ошибки после обнаружения не устраняются. Но согласно нашему допущению о форсировании тактовой частоты величина интенсивности представится как l(B), поэтому
. (5)
Положим
l(B) = l0 + g(B–B0)r, (6)
где
g - коэффициент пропорциональности, а r – коэффициент эффективности форсирования. Величины l(B), g, B, r должны определяться из эксперимента. Коэффициент ускорения испытаний будет равен: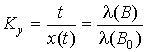
. (7)
Выражение (7) находится из условия
l(B)Ч x(t) =l(B0)Ч t, означающего равенство статистических ресурсов согласно физическому принципу Н.М. Седякина [5].Пример. В результате эксперимента определены: В
1 = 400 МГц/с; В2 = = 500 МГц/с; В3 = 600 МГц/с; В0 = 200 МГц/с; l(B1) = 0,0017 с–1; l(B2) = = 0,0055 с–1; l(B3) = 0,0129 с–1. Составив систему трёх уравнений вида (6) с тремя неизвестными l0, g< r, найдём значения этих величин:l0 = l(B0) = 0,0001 c–1; g = 2Ч 10–10 cr–1Ч оп–r; r = 3.
Коэффициенты ускорения испытаний соответственно равны: Ку
1 = 17; Ку2 = 55; Ку3 = 129. Если потребное время функционирования ПО в штатных условиях t = 10 с, то вероятность безошибочной работы равна Р(10) =е–10Ч 0,0001 = = 0,999. Время форсированных испытаний ПО с быстродействием В=600 опЧ с–1 составит
.
б) Нестационарный процесс Пуассона. Если в процессе испытаний ПО выявлена зависимость интенсивности ошибки от времени, то для её пересчёта к интенсивности ошибки в нормальных условиях необходимо использовать выражение
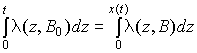, (8)
следующее из равенства вероятностей
pk для различных условий испытаний.Для нахождения
l(t, B0) из (8) дополним данное выражение инвариантом видаB0t = Bx(t), (9)
справедливым с точностью до постоянного множителя для левой и правой частей и означающим постоянство “энергетических затрат” на производство испытаний в двух различных режимах при условии, что израсходованные ПО статистические ресурсы (8) одинаковы. В статье [5] условие (9) названо “линейным энергетическим постулатом”.
Решая (8) и (9) совместно относительно
l(t, B0), получим: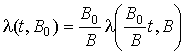
. (10)
Данное выражение и может служить в качестве модели пересчёта результатов форсированных испытаний к нормальным условиям. Нетрудно заметить, что (10) сохраняет инвариантным любое распределение времени до ошибки, т.е. не изменяющим вид закона в зависимости от режима форсирования. Наряду с (10), являющимся самым простым выражением пересчёта, могут быть получены и другие, более сложные выражения, отвечающие другим моделям испытаний.
Пример. В результате форсированных испытаний некоторого ПО установлено: В
0 = 200 МГц/с; В = 600 МГц/с; закон распределения времени между ошибками Вейбулла. Построена кривая интенсивности ошибки ПО в зависимости от врем
ени. С кривой сняты
значения интенсивности: t1 =20 c;
t
=100c; l1(t1) = 5Ч 10–6 с–1; l2(t2) = 10–6 с–1. Интенсивность ошибки для
закона Вейбулла определяется выражением
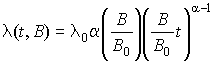, (11)
где
l 0, a - параметры закона, являющиеся неизвестными. Подставляя значения указанных величин в (11) и учитывая, что В/В0 = 3, получим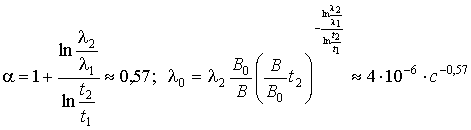
.
Тогда интенсивность ошибки при произвольном быстродействии
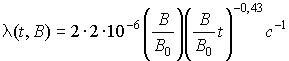. (12)
При нормальном режиме В
= В0, поэтому из (12) получаем
.
Рассмотренный принцип форсированных испытаний ПО нуждается в экспериментальной проверке. Эффективность испытаний различных видов ПО также может быть установлена опытным путём, при этом могут быть предложены другие, более сложные, модели пересчётов результатов испытаний к нормальным условиям эксплуатации.
Список литературы
.
Только подписка гарантирует Вам оперативное получение информации о новинках данного раздела
Нужное: Услуги нянь Коллекционные куклы Уборка, мытье окон
